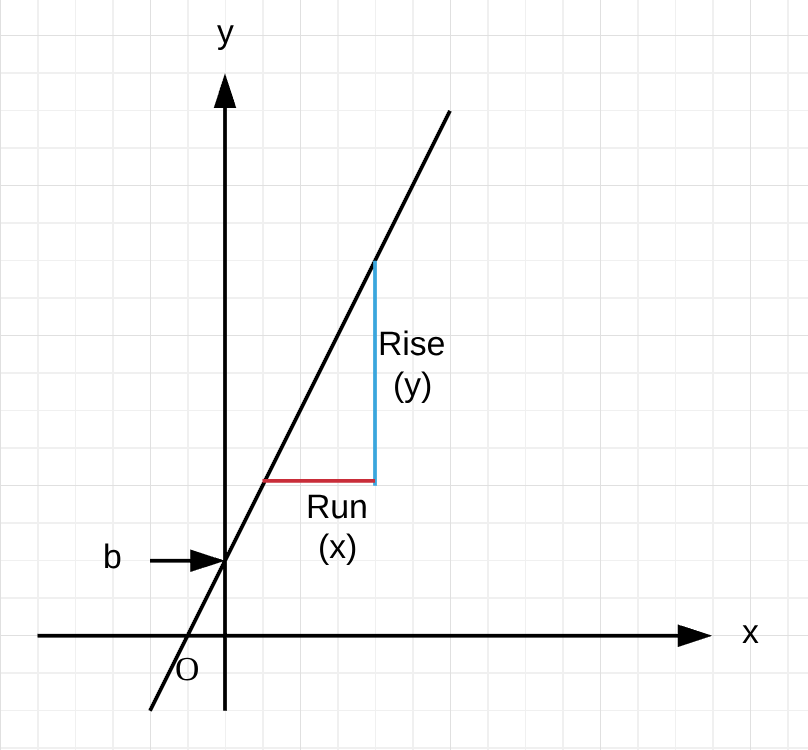
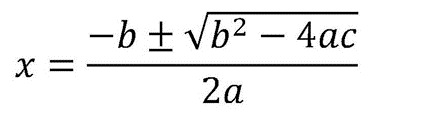 Linear Graph
Linear Graph
Linear Equations
𝒚 = 𝒎𝒙 + 𝒃
𝒎 = gradient and 𝒃 = constant (y-intercept)
How to find 𝒎 and 𝒃:
• 𝒃 is the point where the graph meets the y-axis (or when x=0).
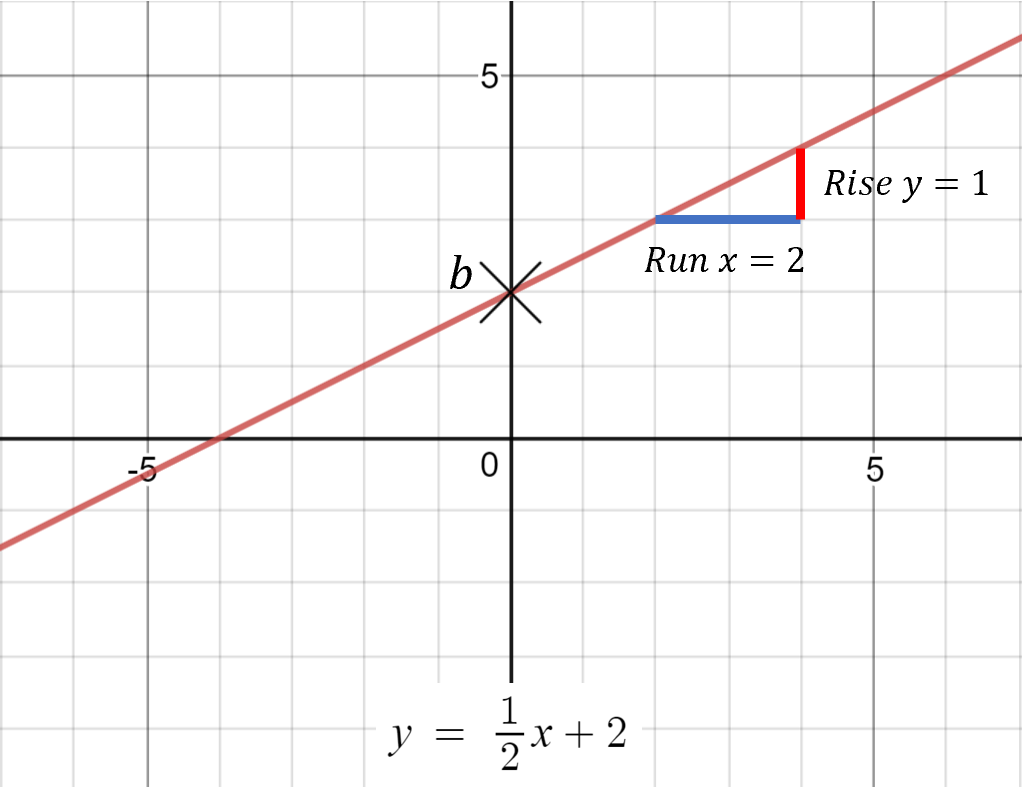 Eg.1 Linear
Eg.1 Linear
Example:
Eg.1: 𝒚 = 1/2𝒙 + 2
• Gradient =
Rise(𝒚) = 1
Run(𝒙) = 2
=
1/
2
• y-intercept: line cuts through the y-axis at (0,2)
Solving without graph: sub x = 0, y = 1/2(0) + 2 = 2, y-int: 2
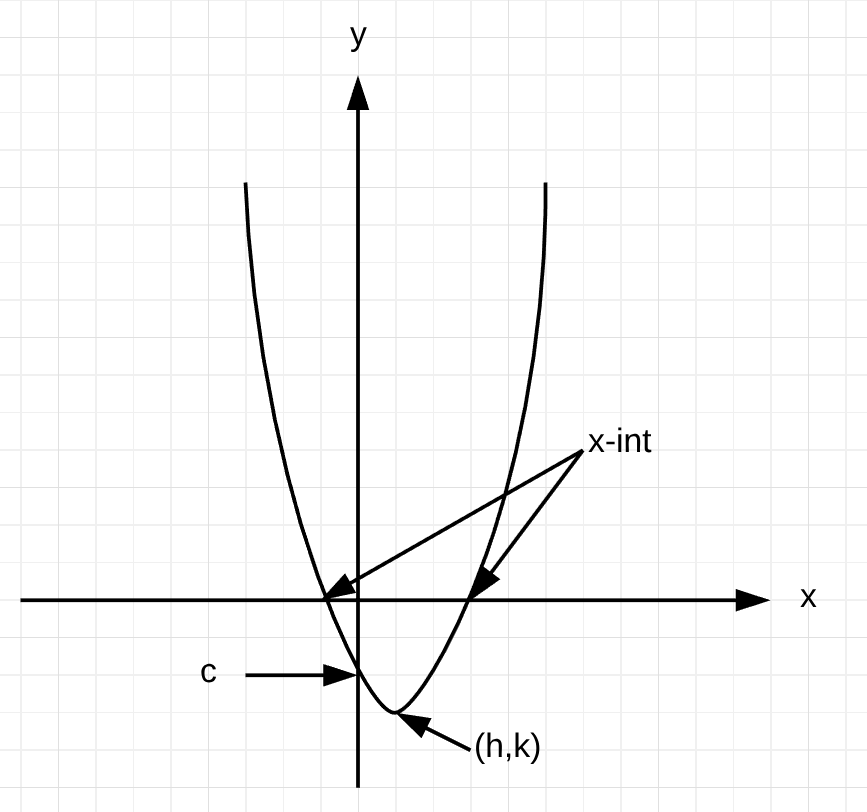 Quadratic Graph
Quadratic Graph
Quadratic Equations
𝒚 = 𝒂𝒙2 + 𝒃𝒙 + 𝒄
𝒄 = constant (y-intercept)
How to find important points:
• Gradient can't be found due to the graph being a curve.
• 𝒄 (y-intercept): Find it the same way as mentioned above. (Sub x = 0)
• x-intercept:
- Step 1, sub y = 0.
- Step 2a, factorise equation if possible and find x (example shown later...), or....
- Step 2b, use the formula below:
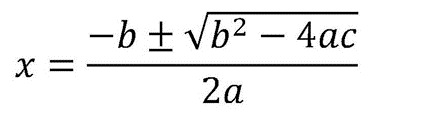
• Vertex (turning point):
- Step 1, convert equation to vertex form,
𝒚 = 𝒂𝒙2 + 𝒃𝒙 + 𝒄 = 𝒂(𝒙 -
𝒉)2 + 𝒌
𝒉 = -𝒃/2𝒂
𝒌 = -(𝒃2 - 4𝒂𝒄)/4𝒂
- Step 2, Vertex = (𝒉,𝒌)
Examples:
 Eg.1: Quadratic
Eg.1: Quadratic
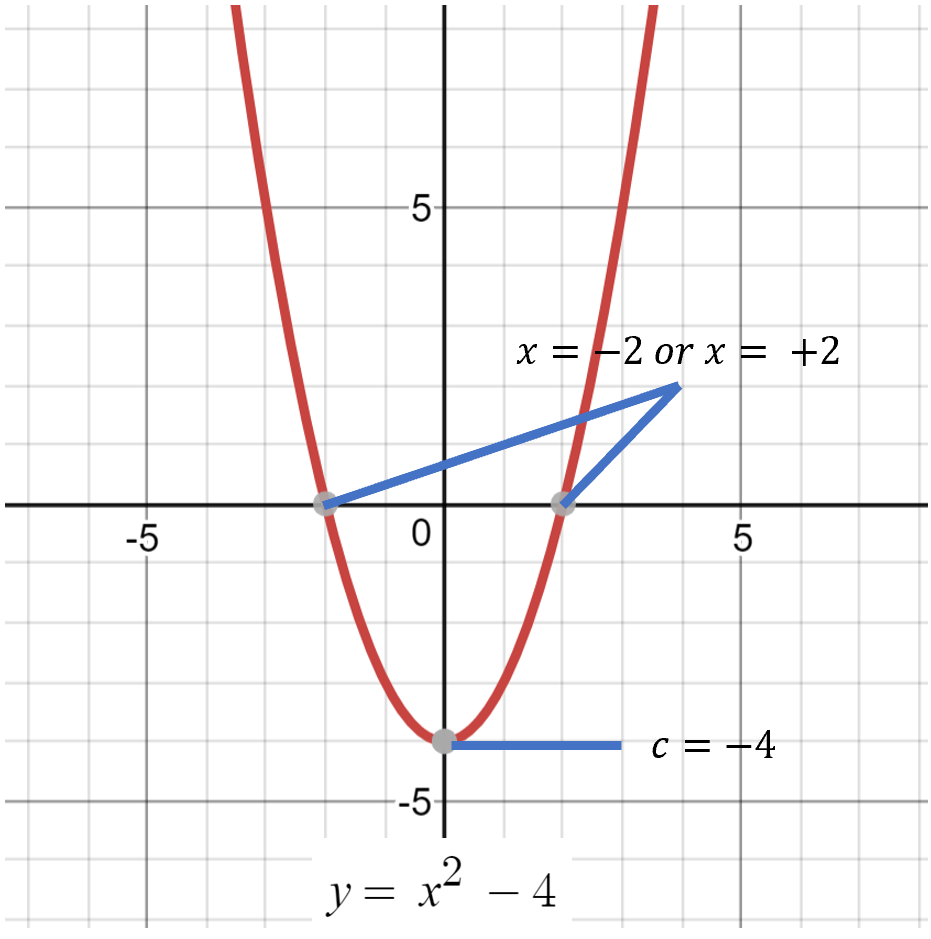
Eg.1: 𝒚 = 𝒙2 - 4
• x-intercept (factorisation method):
When y = 0,
0 = 𝒙2 - 4
0 = (𝒙 + 2)(𝒙 - 2)
𝒙 + 2 = 0 or 𝒙 - 2 = 0
𝒙 = -2 or 𝒙 = +2
x-intercept = (2,0) or (-2,0).
• Vertex:
𝒉 = -0/2 = 0;
𝒌 = -(02 - 4x1x(-4))/4x1 = -4
Vertex = (𝒉,𝒌) = (0,-4).
 Eg.2: Quadratic
Eg.2: Quadratic
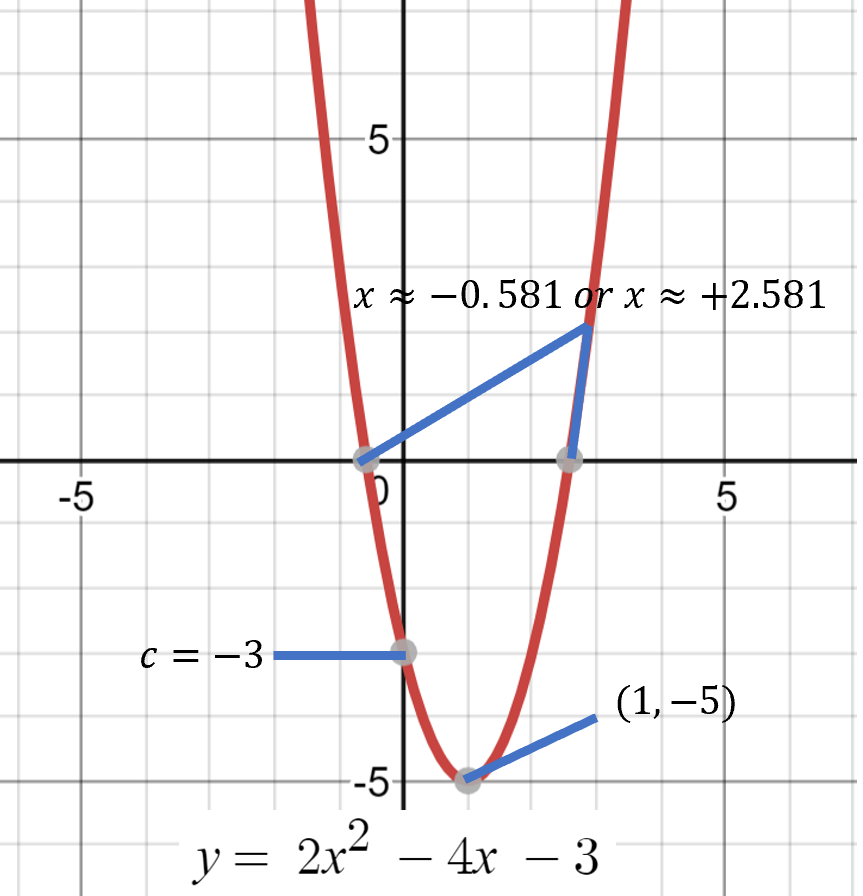
Eg.2: 𝒚 = 2𝒙2 - 4𝒙 - 3
• x-intercept (formula method):
When y = 0,
0 = 2𝒙2 - 4𝒙 - 3
*you can't factorise to get x as a rational number, so using the formula...
𝒙 =
-4 ± √42 - 4(2)(3)
2(2)
𝒙 ≈ +2.581 or 𝒙 ≈ -0.581
x-intercept = (+2.581,0) or (-0.581,0).
• Vertex:
𝒉 = -(-4)/2(2) = 1;
𝒌 = -((-4)2 - 4x2x(-3))/4x2 = -5
Vertex = (𝒉,𝒌) = (1,-5).